6.1 Inner Product, Length, and Orthogonality
Multiplying Vectors
There are two ways to multiply vectors \(u\) and \(v\):
- the cross product \(u \times v\). We will not be discussing cross products in this class.
- the dot product \(u \cdot v\). The dot product is also called the inner product.
The inner product (or dot product) of two \(n \times 1\) vectors \(u\) and \(v\)
\[u = \begin{bmatrix}u_1 \\ u_2 \\ \vdots \\ u_n\end{bmatrix} \qquad v = \begin{bmatrix}v_1 \\ v_2 \\ \vdots \\ v_n\end{bmatrix}\]
is the product \(u \cdot v = u^T v\).
\[u \cdot v = \begin{bmatrix}u_1 & u_2 & \cdots & u_n\end{bmatrix} \begin{bmatrix}v_1 \\ v_2 \\ \vdots \\ v_n\end{bmatrix} = u_1 v_1 +u_2 v_2 + \cdots + u_n v_n\]
IMPORTANT: Notice that when you take the dot product of two vectors you have a scalar answer. The dot product is a single number.
Find \(u \cdot v\) for \(u = \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\) and \(v = \begin{bmatrix}-1 \\ 2 \\ -7\end{bmatrix}\)
Properties of the Inner Product:
Let \(u\), \(v\), and \(w\) be vectors in \(\mathbb{R}^n\), and let \(c\) be a scalar. Then:
- \(u \cdot v = v\cdot u\)
- \((u+v)\cdot w = u \cdot w + v \cdot w\)
- \((c u)\cdot v = c(u\cdot v) = u\cdot (cv)\)
- \(u \cdot u \geq 0\), and \(u \cdot u = 0 \Leftrightarrow u=0\)
Properties 2 and 3 can be combined into:
\[(c_1 u_1 + \cdots +c_p u_p)\cdot w = c_1 (u_1\cdot w) + \cdots +c_p (u_p\cdot w)\]
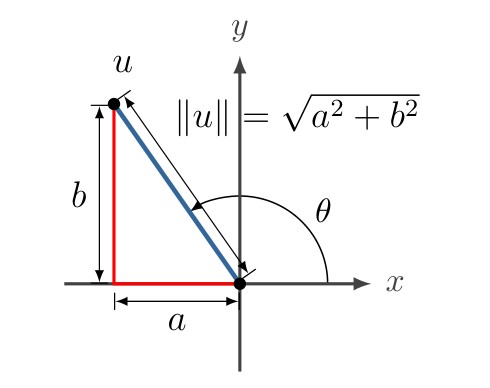
Length of a Vector
The length (or norm) of a vector \(v\) is the nonnegative scalar \(\|v\|\) defined by:
\[\|v\| = \sqrt{v \cdot v} = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}, \qquad \text{and } \|v\|^2 = v\cdot v\]
A unit vector is a vector of length 1.
If \(v\) is a vector the unit vector in the direction of \(v\) is \(\dfrac{v}{\|v\|}\).
The process of changing a vector \(v\) into a unit vector is called normalizing \(v\).
For \(v = \langle -1, 2, -7\rangle\)
- Find the length of \(v\).
- Find a unit vector in the direction of \(v\).
- Write \(v\) as (magnitude) \(\cdot\) (direction) where the direction is a unit vector.
Find the dot product between \(u = \langle 12, 3, -5\rangle\) and \(v = \langle 2, -3, 3\rangle\)
Two vectors \(u\) and \(v\) are orthogonal (perpendicular) to each other if \(u \cdot v = 0\).
Two vectors \(u\) and \(v\) are orthogonal if and only if \(\|u+v\|^2 = \|u\|^2 + \|v\|^2\). (i.e. the Pythagorean theorem is true)
6.2 Orthogonal Sets
A set of vectors \(\{v_1, v_2, \ldots, v_n\}\) is an orthogonal set if each pair of distinct vectors is orthogonal. i.e.: \[v_i \cdot v_j = 0 \qquad \text{for each } i \neq j\]
An orthogonal basis is a basis that is also an orthogonal set.
An orthonormal basis (set) is an orthogonal basis (set) of unit vectors (length 1).
Orthogonal sets are linearly independent.
Show that the following vectors form an orthogonal set.
\[u_1 = \langle 1, -2, 1\rangle, ~~ u_2 = \langle 0, 1, 2\rangle, ~~ u_3 = \langle -5,-2,1\rangle\]
Construct an orthonormal basis from:
\[u_1 = \langle 1, -2, 1\rangle, ~~ u_2 = \langle 0, 1, 2\rangle, ~~ u_3 = \langle -5,-2,1\rangle\]
Orthogonal Projection of One Vector onto Another
The angle \(\theta\) between two vectors, \(u\) and \(v\), can be calculated using the dot product:
\[u \cdot v = \|u\| \|v\| \cos \theta\]
\[\cos \theta =\frac{u \cdot v}{\|u\| \|v\|}\]
We can use the angle and the dot product to find the projection of \(v\) onto \(u\).
\[\hat{v} = \text{proj}_u v = \left(\frac{u \cdot v}{\|u\|^2} \right) u = \left(\frac{u \cdot v}{u \cdot u} \right) u\]
Find the projection of \(v =\begin{bmatrix}5 \\6\end{bmatrix}\) onto:
- \(u_1 = \begin{bmatrix}-2\\1\end{bmatrix}\) and
- \(u_2 = \begin{bmatrix}1 \\ 2\end{bmatrix}\)
- What is the sum of the two projections?
Let \(\{u_1, u_2, \ldots, u_p\}\) be an orthogonal basis for a subspace \(W\) of \(\mathbb{R}^n\). For each \(y \in W\), the weights in:
\[y=c_1 u_1 + c_2 u_2 + \cdots + c_p u_p\]
are given by:
\[c_i = \frac{u_i \cdot y}{u_i \cdot u_i}\]
Note: The weights \(c_i\) are the projections onto each vector in the orthogonal basis.
Write \(y=\begin{bmatrix}6 \\ 1 \\ -8\end{bmatrix}\) as a linear combination of:
\[u_1 = \begin{bmatrix}1 \\ -2 \\ 1\end{bmatrix}, \qquad u_2 = \begin{bmatrix} 0 \\ 1 \\ 2\end{bmatrix}, \qquad u_3 = \begin{bmatrix}-5 \\ -2 \\ 1\end{bmatrix}\]
We showed in example 4 that this is an orthogonal basis.
6.3 Orthogonal Projections
Recall: From section 6.2 we saw that we could project one vector \(\vec{v}\) onto another vector \(\vec{u}\): \(\text{proj}_{\vec{u}} \vec{v}\).
Now we would like to project vector \(\vec{v}\) onto a subspace \(W\) of \(\mathbb{R}^n\): \(\hat{v} = \text{proj}_{W} \vec{v}\). \(\vec{v}\) can be written as a component in \(W\) (\(\hat{v}\)) and a component perpendicular to \(W\) (\(z\)).
The space perpendicular to \(W = \text{span}\{u_1, u_2, \ldots, u_p\}\) is called the orthogonal complement of \(W\) and is written \(W^{\perp}\) (read “\(W\) perpendicular” or simply “\(W\) perp”). Note: \(\mathbb{R}^n = W + W^\perp\)
Show that \(W^{\perp}\) is a subspace of \(\mathbb{R}^n\).
Solution: Start with \(u \in W\) and show:
- zero vector (is \(0 \in W^{\perp}\)?)
- closed under addition. (for \(v \in W^{\perp}\) and \(x \in W^{\perp}\) is \(v +x \in W^{\perp}\)?)
- all other properties inherited from \(\mathbb{R}^n\)
Suppose \(\{u_1, u_2, \ldots, u_n\}\) is an orthogonal basis for \(\mathbb{R}^n\) and \(W=\{u_1, u_2, \ldots, u_p\}\) then any vector \(y\in\mathbb{R}^n\):
\[y=c_1 u_1 + c_2 u_2 + \cdots + c_p u_p + c_{p+1}u_{p+1} + \cdots + c_n u_n\]
where the weights are given by:
\[c_i = \frac{u_i \cdot y}{u_i \cdot u_i}\]
Note: The weights \(c_i\) are the projections onto each vector in the orthogonal basis.
Find the orthogonal projection of \(y\) onto the subspace spanned by \(u_1\) and \(u_2\) where:
\[y = \begin{bmatrix}-1 \\ 4 \\ 3\end{bmatrix}, \qquad u_1 = \begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix}, \qquad u_2 = \begin{bmatrix}-1\\ 1 \\ 0\end{bmatrix}\]
Find \(\hat{y} = \text{proj}_W y = c_1 u_1 +c_2 u_2\)
\(W\) is the subspace spanned by:
\[u_1 = \begin{bmatrix}1 \\ 3 \\ -2\end{bmatrix}, \qquad u_2 = \begin{bmatrix}5 \\ 1 \\ 4\end{bmatrix}\]
Write \(y=\begin{bmatrix}1 \\ 3 \\ 5\end{bmatrix}\) as a sum of a vector in \(W\) and a vector in \(W^\perp\) (i.e. \(y = \hat{y} +z\))
Find the closest point (\(\hat{y}\)) and the shortest distance (\(\|z\|\)) to \(\vec{y} = \begin{bmatrix}3 \\ 1 \\ 5 \\ 1\end{bmatrix}\) in the subspace:
\[W = \{u_1, u_2 \} = \left\{\begin{bmatrix}3 \\ 1 \\ -1 \\ 1\end{bmatrix}, \begin{bmatrix}1 \\ -1 \\ 1 \\ -1\end{bmatrix}\right\}\]
6.4 The Gram-Schmidt Process
The Gram-Schmidt Process is a technique by which, if you are given any basis for a subspace V, you can calculate an orthogonal basis for that subspace. The key step in the Gram-Schmidt Process is the calculation of the orthogonal projection of a vector \(\mathbf{v}\) onto a subspace \(W\), sometimes written as \(\hat{\mathbf{v}} = \text{proj}_W \mathbf{v}\):
Orthogonal Projection
Let \(\{\mathbf{u}_1, \mathbf{u}_2, \ldots ,\mathbf{u}_p\}\) be an orthogonal set of vectors in \(\mathbb{R}^n\) and \(W\) be the subspace spanned by these vectors. Let \(\mathbf{v}\) be any vector in \(\mathbb{R}^n\).
The orthogonal projection of \(\mathbf{v}\) onto \(W\) is given by:
\[\widehat{\mathbf{v}} = \dfrac{\mathbf{v} \cdot \mathbf{u}_1}{\mathbf{u}_1 \cdot \mathbf{u}_1} \mathbf{u}_1 + \dfrac{\mathbf{v} \cdot \mathbf{u}_2}{\mathbf{u}_2 \cdot \mathbf{u}_2} \mathbf{u}_2 + \cdots + \dfrac{\mathbf{v} \cdot \mathbf{u}_p}{\mathbf{u}_p \cdot \mathbf{u}_p} \mathbf{u}_p\]
Let \(\mathbf{u}_1 = \begin{bmatrix}2 \\ 5 \\ -1\end{bmatrix}\), \(\mathbf{u}_2 = \begin{bmatrix}-2 \\ 1 \\ 1\end{bmatrix}\), and \(\mathbf{v} = \begin{bmatrix}1\\2\\3\end{bmatrix}\) and \(W = \text{Span} \{\mathbf{u}_1, \mathbf{u}_2\}\).
Find \(\hat{\mathbf{v}} = \text{proj}_W \mathbf{v}\):
The Gram-Schmidt Process
Let \(\mathfrak{B} = \{\mathbf{v}_1, \mathbf{v}_2, \ldots , \mathbf{v}_p\}\) be any linearly independent set of vectors and let \(V\) be the subspace spanned by \(\mathfrak{B}\). We’ll apply the Gram-Schmidt Process to find an orthogonal (or orthonormal) set of vectors which spans \(V\).
We leave the first vector completely unchanged for now. That is, \(\mathbf{w}_1 = \mathbf{v}_1\).
To find the other vectors, we calculate the projection of \(\mathbf{v}_j\) onto the subspace spanned by \(\{\mathbf{w}_1, \ldots , \mathbf{w}_{j-1}\}\),
\[\hat{\mathbf{v}_j} = \dfrac{\mathbf{v}_j \cdot \mathbf{w}_1}{\mathbf{w}_1 \cdot \mathbf{w}_1} \mathbf{w}_1 + \dfrac{\mathbf{v}_j \cdot \mathbf{w}_2}{\mathbf{w}_2 \cdot \mathbf{w}_2} \mathbf{w}_2 + \cdots + \dfrac{\mathbf{v}_j \cdot \mathbf{w}_{j-1}}{\mathbf{w}_{j-1} \cdot \mathbf{w}_{j-1}} \mathbf{w}_{j-1}\]
then set \(\mathbf{w}_j = \mathbf{v}_j - \hat{\mathbf{v}}_j\). (Optional: You may multiply \(\mathbf{w}_j\) by the lowest common denominator of its components if that helps.)
- The set \(\{\mathbf{w}_1, \ldots , \mathbf{w}_{p}\}\) is an orthogonal basis for \(W\).
If you want an orthonormal basis for \(W\) then continue as follows:
Once the vectors \(\{\mathbf{w}_1, \ldots , \mathbf{w}_{p}\}\) have been computed, scale them to a length of 1: \(\mathbf{u}_j = \dfrac{\mathbf{w}_j}{\|\mathbf{w}_j\|}\)
The set \(\{\mathbf{u}_1, \ldots , \mathbf{u}_{p}\}\) is an orthonormal basis for \(V\)
Find an orthonormal basis for \(W = \text{Span} \left\{ \begin{bmatrix}0\\4\\2\end{bmatrix}, \begin{bmatrix}5\\6\\ -7\end{bmatrix} \right\}\)
Find an orthogonal basis for Col \(A\) where:
\[A=\begin{bmatrix}3&-5&1 \\ 1&1&1 \\-1 & 5 & -2 \\ 3 & -7 & 8\end{bmatrix}\]
Answer: \(\begin{bmatrix}3\\1\\-1\\3\end{bmatrix}, \begin{bmatrix}1\\3\\3\\-1\end{bmatrix}, \begin{bmatrix}-3\\1\\1\\3\end{bmatrix}\)
Find an orthogonal basis for:
\[\mathfrak{B} = \text{Span} \left\{ \begin{bmatrix}1\\-1\\-1\\1\\1\end{bmatrix}, \begin{bmatrix}2\\1\\4\\-4\\2\end{bmatrix}, \begin{bmatrix}5\\-4\\-3\\7\\1\end{bmatrix} \right\}\]
Answer: \(\begin{bmatrix}1\\-1\\-1\\1\\1\end{bmatrix}, \begin{bmatrix}3\\0\\3\\-3\\3\end{bmatrix}, \begin{bmatrix}2\\0\\2\\2\\-2\end{bmatrix}\)